Lógica difusa y fuzzy clustering.
overxfl0w13, 03 Apr 2016¿Cómo determinamos si una persona es alta o baja? ¿y si la temperatura resulta fria, agradable o caliente? ¿y si algo es barato o caro?. Lo normal en estos casos, cuando no se conoce la lógica difusa que trataremos en esta entrada, es pensar en separarlo mediante rangos perfectamente delimitados. Pero esto no es lo más adecuado y de hecho, no es lo que más se ajusta al mundo real como veremos.
Lógica difusa
La lógica difusa (fuzzy logic) nos permite lidiar con cualquier tipo de información imprecisa e.g. datos conocidos aproximadamente, precisión en las medidas, etc
Un caso particular de este tipo de lógica son los conjuntos difusos (Zadeh, 1979). La diferencia entre los conjuntos clásicos y los conjuntos difusos radica en la forma de afirmar si un elemento pertenece a un conjunto. Más concretamente:
- Conjuntos clásicos: un elemento pertenece, o no pertenece a un conjunto.
- Predicado de pertenencia
- Predicado de pertenencia
- Conjuntos difusos: un elemento pertenece en mayor o menor medida a un conjunto (la frontera de los cojuntos es difusa).
- Función de pertenencia
- Función de pertenencia
Para ver un caso más claro, tomaremos el ejemplo de la estatura mencionado al principio de la entrada. Si lo dividimos de la forma trivial usando rangos bien delimitados, podríamos considerar algo así:
- [-inf,1.60] : Baja
- [1.61,1.75] : Media
- [1.75,inf] : Alta
Realmente, si una persona que mide 1.75 crece 1cm, ¿pasa a ser alta de repente?. Podemos considerar que dicha persona tiene una posibilidad de pertenencia a Baja de 0.25 , a Media de 0.9 y a Alta de 0.25 (hay que tener presente que se habla de posibilidades de pertenencia no de probabilidades - los conjuntos difusos inducen una distribución de posibilidades -, de ello se encarga el razonamiento probabilístico).
Estas funciones de pertenencia se suelen especificar mediante funciones f que se ajusten a trapecios (no tienen porque ser únicamente trapecios), definiendo cada una de estas funciones un conjunto difuso - partición -. (Ejemplo). Deben cumplir 2 propiedades:
-
Completitud: garantizar que ningún valor quede excluido de todas las particiones fuzzy, por lo que dado cualquier elemento del universo U empleado, su posibilidad de pertenencia debe ser >0 en alguna de las particiones.
-
Partición fuerte: la suma de las funciones de pertenencia de un elemento de U en cada una de las particiones es 1.
También es posible modificar las funciones de pertenencia para tener en cuenta conceptos más complejos modificando los valores difusos e.g. X es extremadamente A, X es más o menos A, etc. Estos modificadores se denominan modificadores linguísticos y existen estándares para su definición. Algunos ejemplos son éstos.
Del mismo modo que sobre los conjuntos clásicos hay definidas una serie de operaciones, también las hay en los conjuntos difusos, dados 2 conjuntos difusos A y B, se definen:
-
Igualdad de conjuntos (A=B): decimos que 2 conjuntos A y B son iguales cuando para todo elemento x del universo U las funciones de pertenencia de x en ambos vale lo mismo
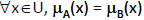
-
Complemento: El complementario de un elemento x en un conjunto difuso A es 1 - la función de pertenencia de x al conjunto A
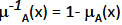
-
Inclusión (A contenido en B): Decimos que A está contenido en B cuando para todo elemento x del universo U la función de pertenencia de x en A es menor o igual que la función de pertenencia de x en B
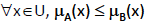
-
Intersección (A intersección B):
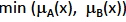
-
Unión (A unión B):
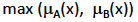
También se definen operaciones aritméticas como: suma, resta, multiplicación y división, que no comentaremos en esta entrada porque no nos serán de utilidad para el caso páctico de clustering difuso, tampoco veremos otros aspectos clave como el proceso de inferencia difusa aplicando reglas y hechos difusos por el mismo motivo, sin embargo, es muy posible que comente en próximas entradas todos esos aspectos.
Por último, destacar que este tipo de métodos está muy extendido y son muchos los dispositivos y aplicaciones que hacen uso de dichos métodos, algunos de ellos son:
- Control de spam (Mozilla)
- Cámara autofoco (Canon)
- Control de frenado
- Acondicionador de aire doméstico (Mitsubishi)
- Aprendizaje automático (e.g. clustering difuso)
Fuzzy clustering
[TODO]
Si tienes alguna duda, comentario o sugerencia, notifícanos a través de indeseables.git@gmail.com y si te ha gustado la entrada puedes compartirla!.
